Необходимый объем данных и ошибки в процессе наблюдений

При экспериментальном исследовании дорожного движения важно обеспечить достаточный объем информации для объективной оценки изучаемого параметра. Перед исследователем всегда стоит задача выполнить наблюдения с наименьшими затратами времени и средств.

Первой задачей обоснования является принятие уровня доверительной вероятности (надежности), достаточного для решения поставленной задачи.

Соответственно выбранному значению надежности Bi устанавливают показатель надежности:

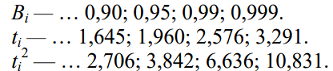
В практике исследований характеристик движения обычно оперируют данными наблюдений, получаемыми с надежностью 0,90…0,95. Это означает, что значение исследуемого параметра будет получено с ошибкой не более 10 %.

Диапазон доверительного интервала зависит от размаха значений наблюдаемого показателя и числа наблюдений. Доверительные границы устанавливают исходя из значения функции ti, которая и характеризует степень требуемой надежности исследуемого параметра. Это значение ti показывает число средних квадратических отклонений

которые нужно отложить вправо и влево от центра рассеивания (среднего значения).

Многочисленными наблюдениями установлено, что для большинства практических расчетов вполне достаточно, чтобы исследуемый показатель находился в пределах:

от своего среднего  значения. Следовательно, размах значений показателя:

отсюда среднеквадратическое отклонение:

Минимально необходимое число наблюдений определяется по формуле:

где Δ — точность измерений, определяемая точностью прибора, используемого при наблюдениях.

Всякое статистическое наблюдение ставит задачу получения таких данных, которые по возможности более точно отображали бы действительность. Под точностью статистической информации  понимается уровень соответствия зафиксированной при натурном наблюдении величины изучаемого признака его действительному значению.

Отклонения между зафиксированными при натурном наблюдении величинами изучаемого признака и действительными его величинами называют ошибками наблюдения.

Ошибки регистрации (технические ошибки), связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п. Они имеют место, как при сплошном, так и не сплошном наблюдении. Ошибки регистрации подразделяются на случайные и систематические.

Случайные ошибки — это ошибки, допущенные при заполнении бланков (цифра записана не в ту графу или допущена описка в записи, оговорка в ответах, нечеткость в вопросе или ответе и т. д.). Случайная ошибка с увеличением объема выборки уменьшается.

Ошибки репрезентативности (представительности) свойственны не сплошному наблюдению. Например: при исследовании интенсивности движения транспортного потока делается вынужденный перерыв, а потом, данные объединяются, как непрерывные.

Наиболее простым и точно отображающим действительность (в большинстве случаев) является, нормальный закон распределения ошибок (рис. 7.7).

Величина S2 называется дисперсией данного нормального закона.

Чем больше значение коэффициента вариации, тем относительно больший разброс и меньшая выравненность исследуемых значений.

В выборочном наблюдении используются понятия «генеральная совокупность» — совокупность единиц, подлежащая изучению по интересующим исследователя признакам, и «выборочная совокупность» — случайно выбранная из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, т. е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности.

Исследователя могут интересовать и распределение единиц по изучаемым признакам в генеральной и выборочной совокупностях. В этом случае частоты называются соответственно генеральными и выборочными.

Теоретическим обоснованием научной работы со случайными ошибками выборки является теория вероятностей и ее предельные теоремы.